(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
| 射手甲 |
射手乙 |
||||||
| 环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
| 概率 |
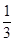 |
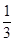 |
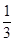 |
概率 |
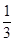 |
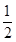 |
 |
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为 ,求
,求 的分布列和期望.
的分布列和期望.
相关知识点
推荐套卷
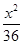 +
+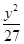 =1有相同焦点,且经过点(4,
=1有相同焦点,且经过点(4, ).
).
 ,其中
,其中 .
. 的单调区间;
的单调区间; <
<
 粤公网安备 44130202000953号
粤公网安备 44130202000953号