如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC边上于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式。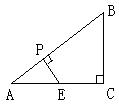
相关知识点
推荐套卷
如图,在△ABC中,∠C=90°,P为AB上一点,且点P不与点A重合,过点P作PE⊥AB交AC边上于E点,点E不与点C重合,若AB=10,AC=8,设AP的长为x,四边形PECB的周长为y,求y与x之间的函数关系式。