某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组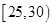 ,第3组
,第3组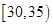 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
相关知识点
推荐套卷
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组 ,第2组
,第2组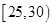 ,第3组
,第3组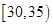 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.