如图,已知正方形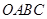 在直角坐标系
在直角坐标系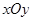 中,点
中,点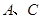 分别在
分别在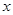 轴、
轴、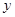 轴的正半轴上,点
轴的正半轴上,点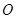 在坐标原点.等腰直角三角板
在坐标原点.等腰直角三角板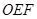 的直角顶点
的直角顶点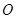 在原点,
在原点,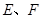 分别在
分别在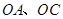 上,且
上,且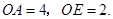 将三角板
将三角板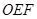 绕
绕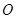 点逆时针旋转至
点逆时针旋转至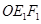 的位置,连结
的位置,连结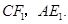
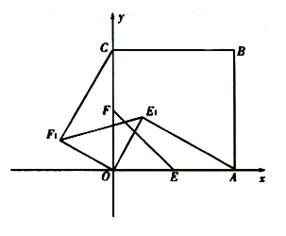
(1)求证: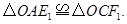
(2)若三角板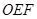 绕
绕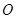 点逆时针旋转一周,是否存在某一位置,使得
点逆时针旋转一周,是否存在某一位置,使得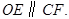 若存在,请求出此时
若存在,请求出此时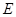 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
如图,已知正方形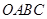 在直角坐标系
在直角坐标系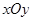 中,点
中,点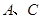 分别在
分别在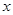 轴、
轴、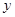 轴的正半轴上,点
轴的正半轴上,点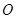 在坐标原点.等腰直角三角板
在坐标原点.等腰直角三角板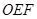 的直角顶点
的直角顶点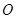 在原点,
在原点,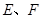 分别在
分别在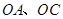 上,且
上,且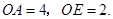 将三角板
将三角板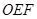 绕
绕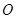 点逆时针旋转至
点逆时针旋转至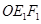 的位置,连结
的位置,连结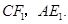

(1)求证: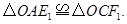
(2)若三角板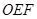 绕
绕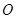 点逆时针旋转一周,是否存在某一位置,使得
点逆时针旋转一周,是否存在某一位置,使得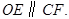 若存在,请求出此时
若存在,请求出此时 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.