如图，在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯，实践证明：桌子边沿处的光的亮度与灯距离桌面的高度AO有关，且当sin∠ABO=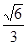
时，桌子边沿处点B的光的亮度最大，设OB=60cm，求此时灯距离桌面的高度OA（结果精确到１cm）．
（参考数据：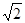
≈１.414；
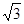≈１.732；
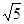≈2.236）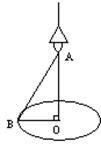
．
．
．
．
．相关知识点
推荐套卷
如图，在一张圆桌(圆心为点O)的正上方点A处吊着一盏照明灯，实践证明：桌子边沿处的光的亮度与灯距离桌面的高度AO有关，且当sin∠ABO=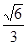时，桌子边沿处点B的光的亮度最大，设OB=60cm，求此时灯距离桌面的高度OA（结果精确到１cm）．
（参考数据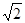：≈１.414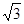；≈１.732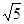；≈2.236）
粤公网安备 44130202000953号