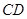 经过
经过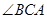 顶点
顶点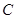 的一条直线,
的一条直线, .
.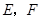 分别是直线
分别是直线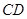 上两点,且
上两点,且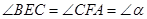 .
.
(1)若直线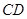 经过
经过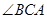 的内部,且
的内部,且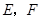 在射线
在射线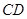 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若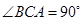 ,
,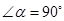 ,
,
则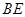
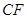 ;
;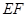
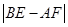 (填“
(填“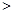 ”,“
”,“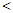 ”或“
”或“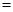 ”);
”);
②如图2,若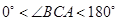 ,请添加一个关于
,请添加一个关于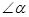 与
与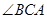 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线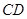 经过
经过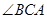 的外部,
的外部,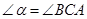 ,请提出
,请提出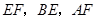 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).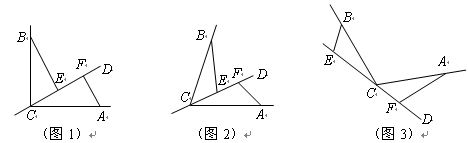
相关知识点
推荐套卷
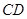 经过
经过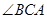 顶点
顶点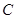 的一条直线,
的一条直线, .
.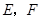 分别是直线
分别是直线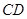 上两点,且
上两点,且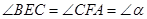 .
.
(1)若直线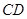 经过
经过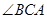 的内部,且
的内部,且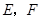 在射线
在射线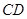 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若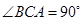 ,
,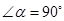 ,
,
则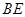
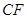 ;
;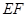
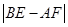 (填“
(填“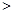 ”,“
”,“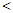 ”或“
”或“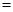 ”);
”);
②如图2,若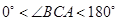 ,请添加一个关于
,请添加一个关于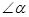 与
与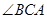 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线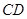 经过
经过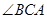 的外部,
的外部,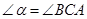 ,请提出
,请提出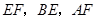 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).