如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设
PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
（I）求证：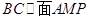
；（Ⅱ）求证：平面MAP⊥平面SAC；
（ Ⅲ）求锐二面角M—AB—C的大小的余弦值；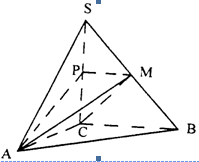
|＝5，|z
|＝2, |z
|＝
，求
的值。
的值域
，求z的模的最大值、最小值。
的最小值.
．推荐套卷
如图，在三棱锥S—ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设
PM=AC=1，∠ACB=90°，直线AM与直线SC所成的角为60°．
（I）求证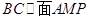：；（Ⅱ）求证：平面MAP⊥平面SAC；
（ Ⅲ）求锐二面角M—AB—C的大小的余弦值；
粤公网安备 44130202000953号