某班组织一次数学测试,全班学生成绩的分布情况如下图: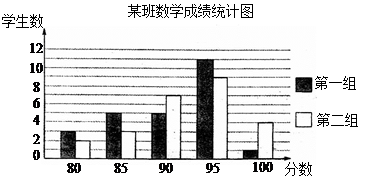
(1)全班学生数学成绩的众数是 分,全班学生数学成绩为众数的有 人.
(2)全班学生数学成绩的中位数是 分.
(3)分别计算两个小组超过全班数学成绩中位数的人数占全班人数的百分比.
相关知识点
推荐套卷
某班组织一次数学测试,全班学生成绩的分布情况如下图:
(1)全班学生数学成绩的众数是 分,全班学生数学成绩为众数的有 人.
(2)全班学生数学成绩的中位数是 分.
(3)分别计算两个小组超过全班数学成绩中位数的人数占全班人数的百分比.