如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF．
下面给出证法1．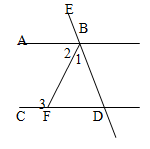
证法1：∠1、∠2、∠3的度数分别为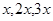
，
∵AB∥CD，∴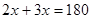
°，解得
，
∴∠1=36°，∠2=72°，∠3=108°，
∵∠EBD=180°，∴∠EBA=72°，
∴BA平分∠EBF．
请阅读证法1后，找出与证法1不同的证法2，并写出证明过程．
相关试题
如图，已知AB∥CD，∠1：∠2：∠3=1：2：3，求证：BA平分∠EBF．
下面给出证法1．
证法1：∠1、∠2、∠3的度数分别为，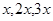
∵AB∥CD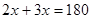，∴°，解得，
∴∠1=36°，∠2=72°，∠3=108°，
∵∠EBD=180°，∴∠EBA=72°，
∴BA平分∠EBF．
请阅读证法1后，找出与证法1不同的证法2，并写出证明过程．
．
的值．
粤公网安备 44130202000953号