已知
是定义在
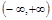上的不恒为零的函数，且对定义域内的任意x, y, f (x)都满足
．
（1）求f (1)、f (-1)的值；
（2）判断f (x)的奇偶性，并说明理由；
（3）证明:
（
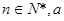为不为零的常数）
，若函数
，其中
，当
时，其值域为
，求实数
的值。
，如果函数
在
上的最大值为
，求
的值。
，
，试比较
与
的大小关系。
的定义域。
的定义域为
，值域为
，且函数
为
的取值范围。相关知识点
推荐套卷
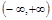已知是定义在上的不恒为零的函数，且对定义域内的任意x, y, f (x)都满足．
（1）求f (1)、f (-1)的值；
（2）判断f (x)的奇偶性，并说明理由；
（3）证明: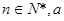（为不为零的常数）
粤公网安备 44130202000953号