(本小题共14分)对于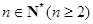 ,定义一个如下数阵:
,定义一个如下数阵: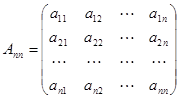
其中对任意的 ,
,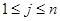 ,当
,当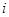 能整除
能整除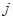 时,
时, ;当
;当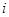 不能整除
不能整除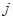 时,
时,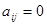 .设
.设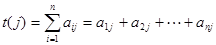 .
.
(Ⅰ)当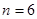 时,试写出数阵
时,试写出数阵 并计算
并计算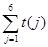 ;
;
(Ⅱ)若 表示不超过
表示不超过 的最大整数,求证:
的最大整数,求证: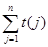
 ;
;
(Ⅲ)若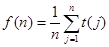 ,
, ,求证:
,求证: .
.
推荐套卷
(本小题共14分)对于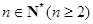 ,定义一个如下数阵:
,定义一个如下数阵: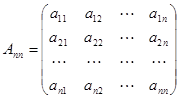
其中对任意的 ,
,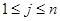 ,当
,当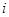 能整除
能整除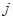 时,
时, ;当
;当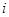 不能整除
不能整除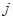 时,
时,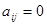 .设
.设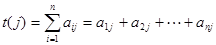 .
.
(Ⅰ)当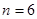 时,试写出数阵
时,试写出数阵 并计算
并计算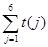 ;
;
(Ⅱ)若 表示不超过
表示不超过 的最大整数,求证:
的最大整数,求证: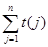
 ;
;
(Ⅲ)若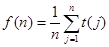 ,
, ,求证:
,求证: .
.