提高南洋大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度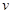 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度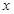 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当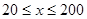 时,车流速度
时,车流速度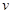 是车流密度
是车流密度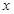 的一次函数.
的一次函数.
(Ⅰ)当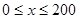 时,求函数
时,求函数 的表达式; (Ⅱ)当车流密度
的表达式; (Ⅱ)当车流密度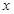 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)  可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
推荐套卷
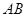 ⊥平面
⊥平面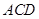 ,
,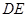 ∥
∥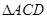 是正三角形,
是正三角形,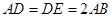 ,且
,且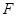 是
是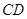 的中点
的中点
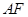 ∥平面
∥平面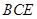 ;
;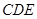 .
.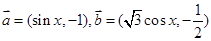 ,函数
,函数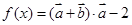 .
.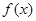 的最小正周期
的最小正周期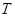 ;
;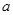 、
、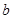 、
、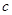 分别为
分别为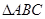 内角
内角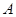 、
、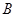 、
、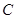 的对边, 其中
的对边, 其中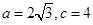 ,且
,且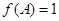 ,求
,求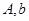 和
和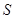 .
. 名,女同学有
名,女同学有 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个 人的课外兴趣小组.
人的课外兴趣小组.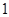 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率; 中,
中,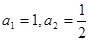 且数列
且数列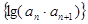 的前n项和
的前n项和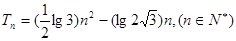 又设
又设 。
。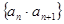 是等比数列;
是等比数列; 的通项
的通项 及前n项和
及前n项和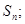
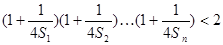
 )的距离比它到X轴的距离多
)的距离比它到X轴的距离多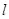 与曲线C交于A、B两点,若
与曲线C交于A、B两点,若  为正三角形,求M点的坐标与直线
为正三角形,求M点的坐标与直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号