(13分)在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合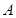 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在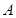 上定义一个运算,记为
上定义一个运算,记为 ,对于
,对于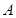 中的任意两个元素
中的任意两个元素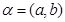 ,
, ,规定:
,规定:
 .
.
(1)计算: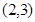

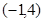 ;
;
(2)请用数学符号语言表述运算 满足交换律,并给出证明;
满足交换律,并给出证明;
(3)若“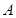 中的元素
中的元素 ”是“对
”是“对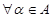 ,都有
,都有


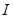

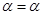 成立”的充要条件,试求出元素
成立”的充要条件,试求出元素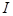 .
.
推荐套卷
(13分)在中学阶段,对许多特定集合(如实数集、复数集以及平面向量集等)的学习常常是以定义运算(如四则运算)和研究运算律为主要内容.现设集合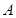 由全体二元有序实数组组成,在
由全体二元有序实数组组成,在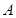 上定义一个运算,记为
上定义一个运算,记为 ,对于
,对于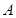 中的任意两个元素
中的任意两个元素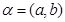 ,
, ,规定:
,规定:
 .
.
(1)计算: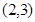

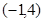 ;
;
(2)请用数学符号语言表述运算 满足交换律,并给出证明;
满足交换律,并给出证明;
(3)若“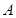 中的元素
中的元素 ”是“对
”是“对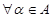 ,都有
,都有


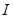

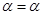 成立”的充要条件,试求出元素
成立”的充要条件,试求出元素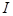 .
.