(本小题满分12分)定义在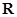 上的函数
上的函数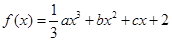 同时满足以下条件:
同时满足以下条件:
①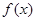 在
在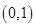 上是减函数,在
上是减函数,在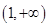 上是增函数;
上是增函数;
②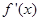 是偶函数;
是偶函数;
③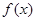 在
在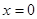 处的切线与直线
处的切线与直线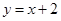 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设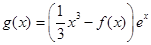 ,求函数
,求函数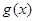 在
在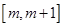 上的最小值.
上的最小值.
相关知识点
推荐套卷
(本小题满分12分)定义在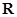 上的函数
上的函数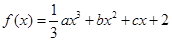 同时满足以下条件:
同时满足以下条件:
①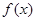 在
在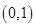 上是减函数,在
上是减函数,在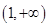 上是增函数;
上是增函数;
②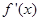 是偶函数;
是偶函数;
③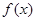 在
在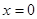 处的切线与直线
处的切线与直线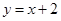 垂直.
垂直.
(1)求函数 的解析式;
的解析式;
(2)设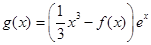 ,求函数
,求函数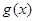 在
在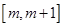 上的最小值.
上的最小值.