在边长为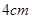
的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥．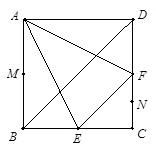
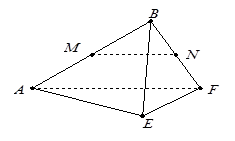
（1）判别MN与平面AEF的位置关系，并给出证明；
（2）证明AB⊥平面BEF；
（3）求多面体E-AFNM的体积．
相关试题
：
的离心率为
，
是椭圆
与椭圆
．且线段
的中点
在圆
上，求
的值．
的三个顶点的坐标为
．
边上的高所在直线的方程；
与
平行，且在
轴上的截距比在
轴上的截距大1，求直线
，若函数
的最小值是
且对称轴是
，
．
的值；
的最小值．
．
是奇函数；
是定义在
上的偶函数，且
时，
．
，
；
，求
的取值范围．相关知识点
推荐套卷
在边长为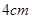的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥．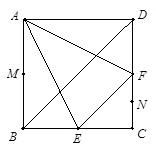
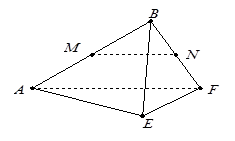
（1）判别MN与平面AEF的位置关系，并给出证明；
（2）证明AB⊥平面BEF；
（3）求多面体E-AFNM的体积．
粤公网安备 44130202000953号