（本小题满分12分）某饮料公司招聘了一名员工，现对其进行一项测试，以使确定工资级别，公司准备了两种不同的饮料共8杯，其颜色完全相同，并且其中4杯为A饮料，另外4杯为B饮料，公司要求此员工一一品尝后，从8杯饮料中选出4杯A饮料，若4杯都选对，则月工资定为3500元，若4杯选对3杯，则月工资定为2800元，否则月工资定为2100元，令X表示此人选对A饮料的杯数，假设此人对A和B两种饮料没有鉴别能力．
（1）求X的分布列；
（2）求此员工月工资的期望.
相关试题
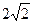，0）和F2（
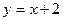交椭圆C于A、B两点，求线段AB的中点坐标。(8分)
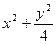=1，求点M（0，1）的直线l交椭圆于点A、B，O为坐标原点，点P满足
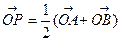，当l绕点M旋转时，求动点P的轨迹方程.如图，已知椭圆C：
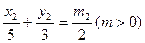，经过椭圆C的右焦点F且斜率为k（k≠0）的直线l交椭圆G于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆于N点．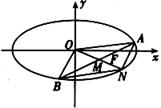
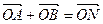（1）是否存在k，使对任意m＞0，总有
成立？若存在，求出所有k的值；
（2）若
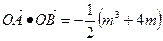，求实数k的取值范围．
已知抛物线的顶点在原点，焦点在y轴的负半轴上，过其上一点
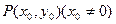的切线方程为
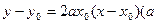为常数）.
（I）求抛物线方程；
（II）斜率为
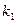的直线PA与抛物线的另一交点为A，斜率为
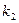的直线PB与抛物线的另一交点为B（A、B两点不同），且满足
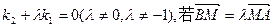，求证线段PM的中点在y轴上；
（III）在（II）的条件下，当
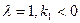时，若P的坐标为（1，－1），求∠PAB为钝角时点A的纵坐标的取值范围.
的左、右焦点分别为
、
，A是椭圆C上的一点，且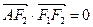
，坐标原点O到直线
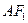的距离为
．
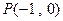，较y轴于点M，若
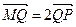，求直线l的方程．相关知识点
推荐套卷
粤公网安备 44130202000953号