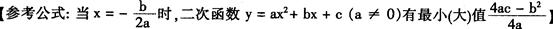小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．
（1）请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
（2）当x是多少时，这个三角形面积S最大?最大面积是多少?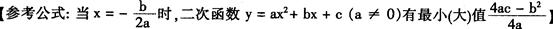
＝－
，其中
相关知识点
推荐套卷
小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．
（1）请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
（2）当x是多少时，这个三角形面积S最大?最大面积是多少?
粤公网安备 44130202000953号