如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝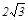
，D、E两点分别在AC、BC上，且DE∥AB，CD＝
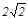．将△CDE绕点C顺时针旋转，得到△CD’E’(如图②，点D’、E’分别与点D、E对应)，点E’在AB上，D’E’与AC相交于点M．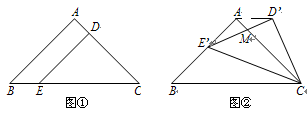
(1)求∠ACE’的度数；
(2)求证：四边形ABCD’是梯形；
(3)求△AD’M的面积．
的一个实数根，求该三角形的面积。
，其中
．相关知识点
推荐套卷
如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC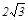＝，D、E两点分别在AC、BC上，且DE∥AB，CD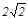＝．将△CDE绕点C顺时针旋转，得到△CD’E’(如图②，点D’、E’分别与点D、E对应)，点E’在AB上，D’E’与AC相交于点M．
(1)求∠ACE’的度数；
(2)求证：四边形ABCD’是梯形；
(3)求△AD’M的面积．
粤公网安备 44130202000953号