如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AC的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于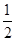 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.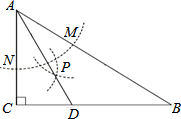
(1)求证:点D在AB的中垂线;
(2)如果△ACD的面积为1,求△ADB的面积.
相关知识点
推荐套卷
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AC的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于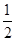 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
(1)求证:点D在AB的中垂线;
(2)如果△ACD的面积为1,求△ADB的面积.