在直角坐标系中,C(2,3),C′(-4,3), C″(2,1),D(-4,1),A(0,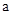 ),B(
),B(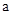 ,O)(
,O)( 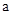
 0).
0).
(1)结合坐标系用坐标填空.
点C与C′关于点 对称; 点C与C″关于点 对称; 点C与D关于点 对称
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求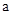 值.
值.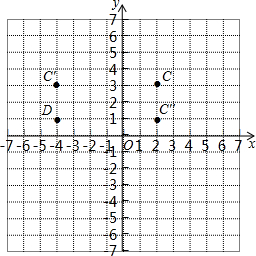
相关知识点
推荐套卷
在直角坐标系中,C(2,3),C′(-4,3), C″(2,1),D(-4,1),A(0,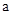 ),B(
),B(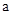 ,O)(
,O)( 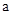
 0).
0).
(1)结合坐标系用坐标填空.
点C与C′关于点 对称; 点C与C″关于点 对称; 点C与D关于点 对称
(2)设点C关于点(4,2)的对称点是点P,若△PAB的面积等于5,求 值.
值.