已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=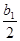 +
+ +
+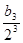 +……+
+……+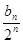 ,(n
,(n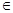 N+),
N+),
求数列{bn}的前n项和Sn。
推荐套卷
已知{an}是一个公差大于0的等差数列,且满足a3a6=55,a2+a7=16。
(1)求数列{an}的通项公式;
(2)若数列{an}和数列{bn}满足等式:an=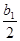 +
+ +
+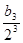 +……+
+……+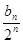 ,(n
,(n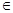 N+),
N+),
求数列{bn}的前n项和Sn。