在某次测验中,有6位同学的平均成绩为75分.用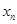 表示编号为
表示编号为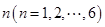 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
成绩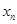 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学成绩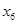 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差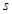 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间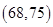 中的概率.
中的概率.
相关知识点
推荐套卷
在某次测验中,有6位同学的平均成绩为75分.用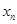 表示编号为
表示编号为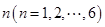 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
成绩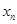 |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学成绩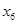 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差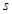 ;
;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间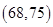 中的概率.
中的概率.