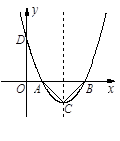一开口向上的抛物线与x轴交于A(m－2，0)，B(m＋2，0)两点，记抛物线顶点为C，且AC⊥BC．
(1)若m为常数，求抛物线的解析式；
(2)若m为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？
(3)设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BOD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．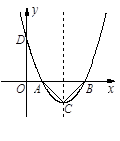
是二元一次方程组
的解，求m+3n的立方根．
，并把解集在数轴上表示出来．相关知识点
推荐套卷
一开口向上的抛物线与x轴交于A(m－2，0)，B(m＋2，0)两点，记抛物线顶点为C，且AC⊥BC．
(1)若m为常数，求抛物线的解析式；
(2)若m为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？
(3)设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BOD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．
粤公网安备 44130202000953号