(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA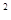 +PB
+PB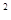 =PC
=PC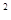 ,证明∠PQC=90°;
,证明∠PQC=90°;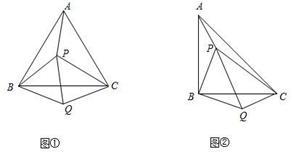
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
相关知识点
推荐套卷
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA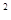 +PB
+PB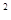 =PC
=PC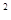 ,证明∠PQC=90°;
,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.