如图，在△ABC中∠BAC=90°,AB=AC=2
,圆A的半径1，点O在BC边上运动（与点B/C不重合），设BO=X,△AOC的面积是y.
⑴求y关于x的函数关系式及自变量的取值范围；
⑵以点O位圆心，BO为半径作圆O，求当○O与○A相切时，△AOC的面积.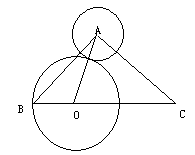
相关知识点
推荐套卷
如图，在△ABC中∠BAC=90°,AB=AC=2,圆A的半径1，点O在BC边上运动（与点B/C不重合），设BO=X,△AOC的面积是y.
⑴求y关于x的函数关系式及自变量的取值范围；
⑵以点O位圆心，BO为半径作圆O，求当○O与○A相切时，△AOC的面积.
粤公网安备 44130202000953号