在交通拥挤地段，为了确保交通安全，规定机动车相互之间的距离d（米）与车
速v（千米/小时）需遵循的关系是
（其中a（米）是车身长,a为常量）,同时
规定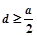
．
（1）当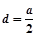
时，求机动车车速的变化范围；
（2）设机动车每小时流量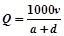
，应规定怎样的车速，使机动车每小时流量Q最大．
相关试题
中，已知
.
的值.[
是边长为4的等边三角形，
是等腰直角三角形，
，平面
平面ABD，且
平面ABC，EC=2.
.
的方程为
，
；求
的值；
轴、
轴上的截距之和等于
；求
满足
.
是等差数列；
，求数列
的前
项和
.
中,角
、
、
所对的边分别是
、
、
,向量
,且
与
共线．
,求
的最大值及此时角推荐套卷
在交通拥挤地段，为了确保交通安全，规定机动车相互之间的距离d（米）与车
速v（千米/小时）需遵循的关系是（其中a（米）是车身长,a为常量）,同时
规定．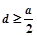
（1）当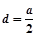时，求机动车车速的变化范围；
（2）设机动车每小时流量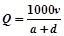，应规定怎样的车速，使机动车每小时流量Q最大．
粤公网安备 44130202000953号