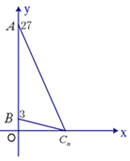
（本小题满分12分）如图，定点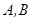
的坐标分别为
，一质点
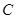从原点出发，始终沿
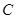轴的正方向运动，已知第1分钟内，质点运动了1个单位，之后每分钟内比上一分钟内多运动了2个单位，记第
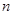分钟内质点运动了
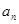个单位，此时质点的位置为
．
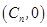（Ⅰ）求、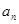
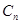的表达式；
（Ⅱ）当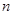为何值时，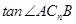
取得最大，最大值为多少？
的零点有且只有一个，求
的值
（
），及
，求
为
的各位数字之和，如
则
，记
，
时，
恒成立，求
的范围相关知识点
推荐套卷
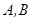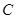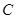（本小题满分12分）如图，定点的坐标分别为，一质点从原点出发，始终沿轴的正方向运动，已知第1分钟内，质点运动了1个单位，之后每分钟内比上一分钟内多运动了2个单位，记第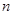分钟内质点运动了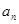个单位，此时质点的位置为．
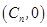（Ⅰ）求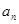、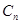的表达式；
（Ⅱ）当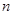为何值时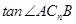，取得最大，最大值为多少？
粤公网安备 44130202000953号