已知某类型的高射炮在它们控制的区域内击中具有某种速度敌机的概率为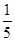 .
.
(Ⅰ)假定有5门这种高射炮控制某个区域,求敌机进入这个区域后被击中的概率;
(Ⅱ)要使敌机一旦进入这个区域内有90%以上的概率被击中,至少需要布置几门这类高射炮?(参考数据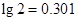 ,
,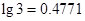 )
)
推荐套卷
已知某类型的高射炮在它们控制的区域内击中具有某种速度敌机的概率为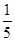 .
.
(Ⅰ)假定有5门这种高射炮控制某个区域,求敌机进入这个区域后被击中的概率;
(Ⅱ)要使敌机一旦进入这个区域内有90%以上的概率被击中,至少需要布置几门这类高射炮?(参考数据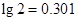 ,
,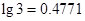 )
)