已知函数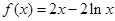
(Ⅰ)求函数在(1,  )的切线方程
)的切线方程
(Ⅱ)求函数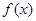 的极值
的极值
(Ⅲ)对于曲线上的不同两点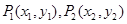 ,如果存在曲线上的点
,如果存在曲线上的点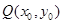 ,且
,且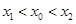 ,使得曲线在点
,使得曲线在点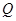 处的切线
处的切线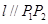 ,则称
,则称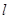 为弦
为弦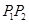 的陪伴切线.
的陪伴切线.
已知两点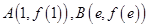 ,试求弦
,试求弦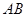 的陪伴切线
的陪伴切线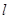 的方程;
的方程;
相关知识点
推荐套卷
已知函数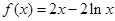
(Ⅰ)求函数在(1,  )的切线方程
)的切线方程
(Ⅱ)求函数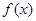 的极值
的极值
(Ⅲ)对于曲线上的不同两点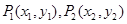 ,如果存在曲线上的点
,如果存在曲线上的点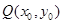 ,且
,且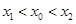 ,使得曲线在点
,使得曲线在点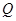 处的切线
处的切线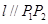 ,则称
,则称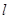 为弦
为弦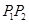 的陪伴切线.
的陪伴切线.
已知两点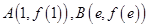 ,试求弦
,试求弦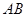 的陪伴切线
的陪伴切线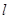 的方程;
的方程;