（本小题满分1
2分）
某市有A、B两所示范高中响应政府号召，对该市甲、乙两个教育落后地区开展支教活动．经上级研究决定：向甲地派出3名A校教师和2名B校教师，向
乙地派出3名A校教师和3名B校教师．由于客观原因，需从拟派往甲、乙两地的教师中各自任选一名互换支教地区．
（Ⅰ）求互换后两校派往两地区教师人数不变的概率；
（Ⅱ）求互换后A校教师派往甲地人数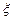
的分布列和数学期望
．
相关试题
中，
，
，
＝
，
＝
，
与
的夹角为
．
，求
、
的值；
的值；
与
的夹角的余弦值．
的图象的一条对称轴是直线
.
求
；
求函数
的单调增区间；
画出函数
上的图象.
,当
为何值时，
与
垂直？
与
是第三象限角，且
.
的值;
的值
的前
项和为
，对任意的正整数
成立，记
。
的通项公式；
，设数列
的前
，求证：对任意正整数
；相关知识点
推荐套卷
（本小题满分12分）
某市有A、B两所示范高中响应政府号召，对该市甲、乙两个教育落后地区开展支教活动．经上级研究决定：向甲地派出3名A校教师和2名B校教师，向乙地派出3名A校教师和3名B校教师．由于客观原因，需从拟派往甲、乙两地的教师中各自任选一名互换支教地区．
（Ⅰ）求互换后两校派往两地区教师人数不变的概率；
（Ⅱ）求互换后A校教师派往甲地人数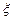的分布列和数学期望．
粤公网安备 44130202000953号