(本小题满分1 2分)
2分)
已知函数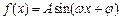 (
(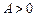 ,
,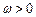 ,
,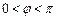
 )在
)在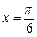 取得最大值2,方程
取得最大值2,方程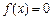 的两个根为
的两个根为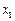 、
、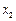 ,且
,且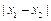 的最小值为
的最小值为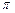 .
.
(Ⅰ)求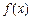 ;
;
(Ⅱ)将函数 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象.当
的图象.当 时,函数
时,函数 (m、n∈R)的值域是
(m、n∈R)的值域是 ,求实数m、n的值.
,求实数m、n的值.
推荐套卷
(本小题满分1 2分)
2分)
已知函数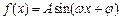 (
(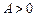 ,
,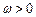 ,
,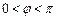
 )在
)在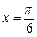 取得最大值2,方程
取得最大值2,方程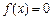 的两个根为
的两个根为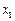 、
、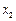 ,且
,且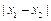 的最小值为
的最小值为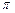 .
.
(Ⅰ)求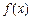 ;
;
(Ⅱ)将函数 图象上各点的横坐标压缩到原来的
图象上各点的横坐标压缩到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数 的图象.当
的图象.当 时,函数
时,函数 (m、n∈R)的值域是
(m、n∈R)的值域是 ,求实数m、n的值.
,求实数m、n的值.