如图所示,直线 与
与 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.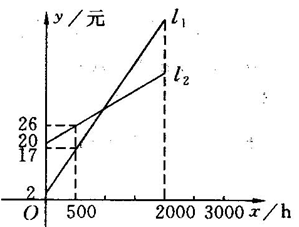
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.
相关知识点
推荐套卷
如图所示,直线 与
与 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
(1)根据图像分别求出L1,L2的函数关系式.
(2)当照明时间为多少时,两种灯的费用相等?
(3)小亮房间计划照明2500h,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法.