如图,抛物线y=ax2+bx+c(a<0)与双曲线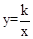 相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC与△ABE的面积;
(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.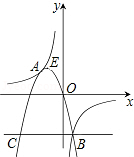
相关知识点
推荐套卷
 ,其中m=1+
,其中m=1+ .
. ;
; .
.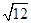 ﹣|
﹣|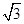 ﹣3|+(
﹣3|+(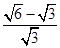 +(2+
+(2+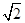 )(2﹣
)(2﹣ 粤公网安备 44130202000953号
粤公网安备 44130202000953号