小张骑车往返于甲、乙两地,距甲地的路程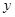 (千米)与时间
(千米)与时间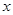 (小时)的函数图象如图所示.
(小时)的函数图象如图所示.
(1)小张在路上停留 小时,他从乙地返回时骑车的速度为 千米/时.
(2)小李与小张同时从甲地出发,按相同路线匀速前往乙地,到乙地停止,途中小李与小张共相遇3次.请在图中画出小李距甲地的路程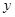 (千米)与时间
(千米)与时间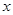 (小时)的函数的大致图象.
(小时)的函数的大致图象.
(3)小王与小张同时出发,按相同路线前往乙地,距甲地的路程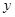 (千米)与时间
(千米)与时间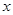 (小时)的函数关系式为
(小时)的函数关系式为 .小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
.小王与小张在途中共相遇几次?请你计算第一次相遇的时间.
相关知识点
推荐套卷
 (k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.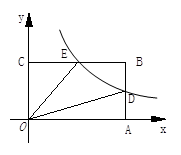
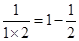
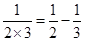
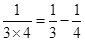 ┅┅
┅┅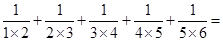 .
.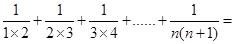 .(用含有
.(用含有 的式子表示)
的式子表示)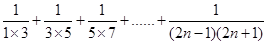 的值为
的值为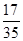 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号