在直角坐标系中，射线OA: x－y=0（x≥0），
OB: x+2y=0（x≥0），过点P(1,0)作直线分别交射线OA、OB于A、B两点.
（1）当AB中点为P时，求直线AB的方程；
（2）当AB中点在直线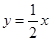
上时，求直线AB的方程.
相关试题
．
的奇偶性，并证明；
的
的取值范围．
；
．
，
．
，求
的取值范围；
，求
，直线
是圆的一条切线，且
与椭圆
交于不同的两点
．
与
的关系；
的长为
，求直线
及圆
．
过点
且被圆
截得的线段
长为
，求直线推荐套卷
在直角坐标系中，射线OA: x－y=0（x≥0），
OB: x+2y=0（x≥0），过点P(1,0)作直线分别交射线OA、OB于A、B两点.
（1）当AB中点为P时，求直线AB的方程；
（2）当AB中点在直线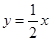上时，求直线AB的方程.
粤公网安备 44130202000953号