如图,在△ABC中,AB=AC,若将△ABC沿CA的方向平移CA的长,得△EFA,
⑴若△ABC的面积为3cm2,求四边形BCEF的面积
⑵试猜想AF与BE有何关系?
⑶若∠BAC=60°,求∠FEB的度数。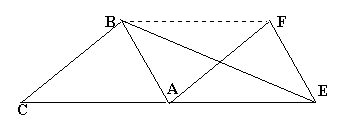
相关知识点
推荐套卷
如图,在△ABC中,AB=AC,若将△ABC沿CA的方向平移CA的长,得△EFA,
⑴若△ABC的面积为3cm2,求四边形BCEF的面积
⑵试猜想AF与BE有何关系?
⑶若∠BAC=60°,求∠FEB的度数。