在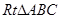 中,
中, ,
, ,
,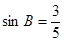 ,⊙
,⊙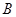 的半径长为1,⊙
的半径长为1,⊙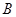 交边
交边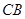 于点
于点 ,
,
点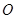 是边
是边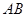 上的动点.
上的动点.
(1)如图1,将⊙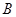 绕点
绕点 旋转
旋转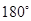 得到⊙
得到⊙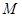 ,请判断⊙
,请判断⊙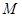 与直线
与直线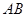 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求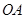 的长;
的长;
(3)如图3,点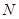 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙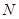 和以
和以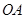 为半径的⊙
为半径的⊙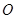 外切,设
外切,设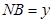 ,
, ,求
,求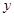 关于
关于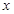 的函数关系式及定义域..
的函数关系式及定义域..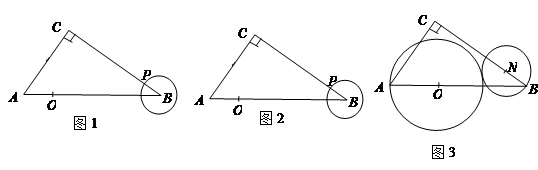
相关知识点
推荐套卷
在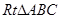 中,
中, ,
, ,
,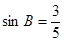 ,⊙
,⊙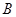 的半径长为1,⊙
的半径长为1,⊙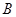 交边
交边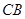 于点
于点 ,
,
点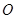 是边
是边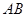 上的动点.
上的动点.
(1)如图1,将⊙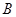 绕点
绕点 旋转
旋转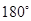 得到⊙
得到⊙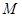 ,请判断⊙
,请判断⊙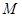 与直线
与直线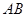 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求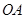 的长;
的长;
(3)如图3,点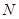 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙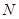 和以
和以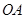 为半径的⊙
为半径的⊙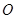 外切,设
外切,设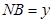 ,
, ,求
,求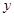 关于
关于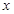 的函数关系式及定义域..
的函数关系式及定义域..