规定:在平面内,如果一个图形绕一个定点旋转一定的角度
后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度
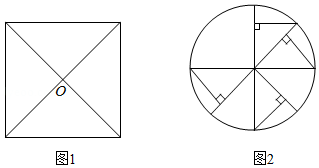
称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点
旋转
或
后,能与自身重合(如图
,所以正方形是旋转对称图形,且有两个旋转角.
根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是 ;
.矩形
.正五边形
.菱形
.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有: (填序号);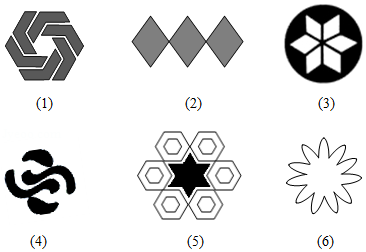
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形.
其中真命题的个数有 个;
.0
.1
.2
.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有
,
,
,
,将图形补充完整.