在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为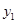 、
、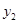 (km),
(km),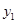 、
、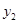 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)甲、乙两船同在行驶途中,若两船距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
相关知识点
推荐套卷
在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为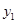 、
、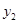 (km),
(km),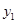 、
、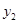 与x的函数关系如图所示.
与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km, ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)甲、乙两船同在行驶途中,若两船距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.