非空集合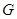 关于运算
关于运算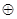 满足:
满足:
(1)对任意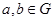 ,都有
,都有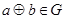 ;
;
(2)存在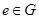 ,使得对一切
,使得对一切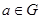 ,都有
,都有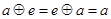 ,则称
,则称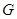 关于运算
关于运算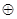 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算: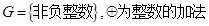
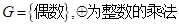 ① ②
① ②
③ 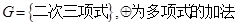
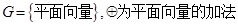 ④
④ 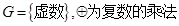 ⑤
⑤
其中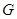 关于运算
关于运算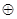 为“融洽集”____________。(写出所有“融洽集”的序号)
为“融洽集”____________。(写出所有“融洽集”的序号)
推荐套卷
非空集合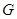 关于运算
关于运算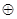 满足:
满足:
(1)对任意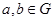 ,都有
,都有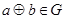 ;
;
(2)存在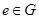 ,使得对一切
,使得对一切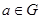 ,都有
,都有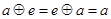 ,则称
,则称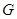 关于运算
关于运算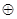 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算: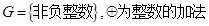
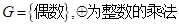 ① ②
① ②
③ 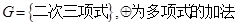
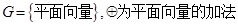 ④
④ 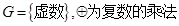 ⑤
⑤
其中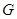 关于运算
关于运算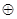 为“融洽集”____________。(写出所有“融洽集”的序号)
为“融洽集”____________。(写出所有“融洽集”的序号)