某车间生产某机器的两种配件A和B，生产配件A成本费y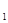
与该车间的工人人数x成反比，而生产配件B成本费y
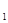与该车间的工人人数x成正比，如果该车间的工人人数为10人时，这两项费用y和y分别为2万元和8万元，那么要使这两项费用之和最小，该车间的工人人数x应为多少？
相关试题
，且与直线2x-y+4=0的交点在x轴上的直线的方程。
的直线的方程.推荐套卷
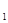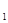某车间生产某机器的两种配件A和B，生产配件A成本费y与该车间的工人人数x成反比，而生产配件B成本费y与该车间的工人人数x成正比，如果该车间的工人人数为10人时，这两项费用y和y分别为2万元和8万元，那么要使这两项费用之和最小，该车间的工人人数x应为多少？
粤公网安备 44130202000953号