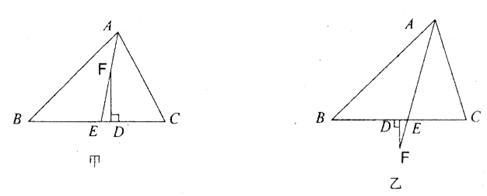
(1)已知:如图1,在△ABC中,D、F分别是AB、CA上的两个定点,在BC上找一点E,使△DEF的周长最小,请作出相应图形并写出作法,
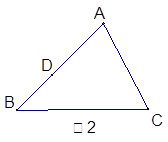
(2)已知:如图2,在△ABC中,若在上一题的条件改为D是AB上一定点,在BC、 CA、上分别找一点E、F使△DEF的周长最小,请作出相应图形并写出作法
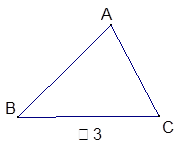
(3)已知:如图3,在△ABC中,是否存在D、E、F分别在AB、BC、CA,且
△DEF的周长最小,若存在请作出相应图形并写出作法,若不存在,请说明理由。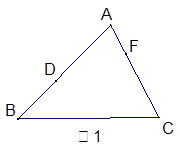
相关知识点
推荐套卷

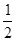 (∠C-∠B);
(∠C-∠B);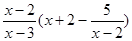 ,再从不等式
,再从不等式 中选取一个合适的整数代入求值。
中选取一个合适的整数代入求值。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号