已知椭圆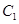 :
: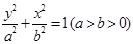 的右顶点为
的右顶点为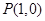 ,过
,过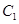 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为 .
.
(I)求椭圆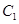 的方程;
的方程;
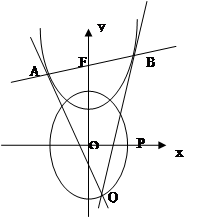
(II)设抛物线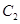 :
: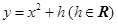 的焦点为F,过F点的直线
的焦点为F,过F点的直线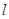 交抛物线与A、B两点,过A、B两点分别作抛物线
交抛物线与A、B两点,过A、B两点分别作抛物线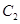 的切线交于Q点,且Q点在椭圆
的切线交于Q点,且Q点在椭圆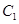 上,求
上,求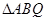 面积的最值,并求出取得最值时的抛物线
面积的最值,并求出取得最值时的抛物线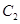 的方程。
的方程。
推荐套卷
已知椭圆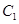 :
: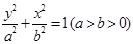 的右顶点为
的右顶点为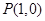 ,过
,过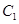 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为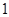 .
.
(I)求椭圆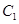 的方程;
的方程;
(II)设抛物线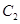 :
: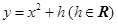 的焦点为F,过F点的直线
的焦点为F,过F点的直线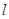 交抛物线与A、B两点,过A、B两点分别作抛物线
交抛物线与A、B两点,过A、B两点分别作抛物线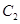 的切线交于Q点,且Q点在椭圆
的切线交于Q点,且Q点在椭圆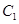 上,求
上,求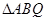 面积的最值,并求出取得最值时的抛物线
面积的最值,并求出取得最值时的抛物线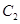 的方程。
的方程。