如图1, E, F，G分别是边长为2的正方形所ABCD所在边的中点，沿EF将ΔCEF截去后，又沿EG将多边形ABEFD折起，使得平面DGEF丄平面ABEG得到如图2所示的多面体.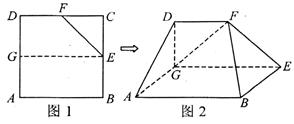
(1) 求证：FG丄平面BEF；
(2) 求二面角A-BF-E的大小；
(3) 求多面体ADG—BFE的体积.
相关试题
在
处取得极值.
；
，如果
在开区间
上存在极小值，求实数
的取值范围.
，
．
的值；
，
，
，求
的值
的定义域为
，且
上是增函数, 是否存在实数
使得
, 对一切
都成立？若存在，求出实数
的对边分别是
，已知
. 
的值；
，求边
的值.
相关知识点
推荐套卷
如图1, E, F，G分别是边长为2的正方形所ABCD所在边的中点，沿EF将ΔCEF截去后，又沿EG将多边形ABEFD折起，使得平面DGEF丄平面ABEG得到如图2所示的多面体.
(1) 求证：FG丄平面BEF；
(2) 求二面角A-BF-E的大小；
(3) 求多面体ADG—BFE的体积.
粤公网安备 44130202000953号