(12分)在德国不来梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形展品,其中第一堆只有一层,就一个球,第2、3、4、…堆最底层(第一层)分别按下图方式固定摆放,从第二层开始每层的小球自然垒放在下一层之上,第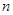 堆的第
堆的第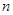 层就放一个乒乓球,以
层就放一个乒乓球,以 表示第
表示第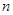 堆的乒乓球总数.
堆的乒乓球总数.


(1)求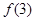 ;
;
(2)求 (用
(用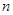 表示)(可能用到的公式:
表示)(可能用到的公式: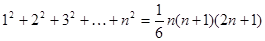 )
)
相关知识点
推荐套卷
(12分)在德国不来梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形展品,其中第一堆只有一层,就一个球,第2、3、4、…堆最底层(第一层)分别按下图方式固定摆放,从第二层开始每层的小球自然垒放在下一层之上,第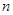 堆的第
堆的第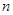 层就放一个乒乓球,以
层就放一个乒乓球,以 表示第
表示第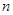 堆的乒乓球总数.
堆的乒乓球总数.


(1)求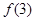 ;
;
(2)求 (用
(用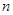 表示)(可能用到的公式:
表示)(可能用到的公式: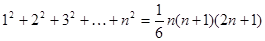 )
)