设函数f(x)=loga(x－3a)，g(x)=loga
，(a>0且a≠1).
(1)若
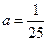，当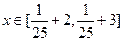
时，求证：|f(x)－g(x)|
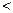1；
(2)当x∈［a+2,a+3］时，恒有|f(x)－g(x)|
1,试确定a的取值范围.
相关试题
，
，
是常数．
的图象在点
处的切线方程；
的取值范围；
．
；
．
的前
项和为
，
.
，
＝
，记数列
的前
.若对
，
恒成立，求实数
的取值范围．
的最大值，并写出使
中，角A、B、C的对边分别为a、b、c，若
，求a的最小值.
的解集；
的解集非空，求实数
的取值范围.推荐套卷
设函数f(x)=loga(x－3a)，g(x)=loga ，(a>0且a≠1).
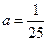(1)若，当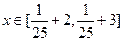时，求证：|f(x)－g(x)|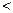1；
(2)当x∈［a+2,a+3］时，恒有|f(x)－g(x)|1,试确定a的取值范围.
粤公网安备 44130202000953号