如图，在Rt△ABC中，∠ACB=90°，AC=6㎝，BC=8㎝，P为BC的中点．动点Q从点P出发，沿射线PC方向以2㎝/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．
⑴当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；
⑵已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．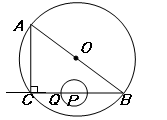
相关试题
.
（填“大于”或“小于”）.
现在要将绿地扩充成等腰三角形，且扩充部分是以
为直角边的直角三角形，求扩充后等腰三角形绿地的周长．
相关知识点
推荐套卷
如图，在Rt△ABC中，∠ACB=90°，AC=6㎝，BC=8㎝，P为BC的中点．动点Q从点P出发，沿射线PC方向以2㎝/s的速度运动，以P为圆心，PQ长为半径作圆．设点Q运动的时间为t s．
⑴当t=1.2时，判断直线AB与⊙P的位置关系，并说明理由；
⑵已知⊙O为△ABC的外接圆，若⊙P与⊙O相切，求t的值．
粤公网安备 44130202000953号