已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．
（1）如图1，若点C（x，0）且-1＜x＜3，BC⊥AC，求y与x之间的函数关系式；
（2）在（1）的条件下，y是否有最大值？若有，请求出最大值；若没有，请说明理由；
（3）如图2，当点B的坐标为（-1，1）时，在x轴上另取两点E，F，且EF=1．线段EF在x轴上平移，线段EF平移至何处时，四边形ABEF的周长最小？求出此时点E的坐标．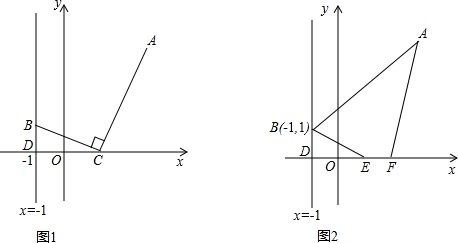
的两个根，求双曲线的函数解析式。
时，它的密度
与V的函数关系式；
时二氧化碳的密度
：
与
平行且过点（3，4），求
，而
与
成反比例，
与
成正比例，并且
时，
；
时，
是反比例函数，求其函数解析式。相关知识点
推荐套卷
已知点A（3，4），点B为直线x=-1上的动点，设B（-1，y）．
（1）如图1，若点C（x，0）且-1＜x＜3，BC⊥AC，求y与x之间的函数关系式；
（2）在（1）的条件下，y是否有最大值？若有，请求出最大值；若没有，请说明理由；
（3）如图2，当点B的坐标为（-1，1）时，在x轴上另取两点E，F，且EF=1．线段EF在x轴上平移，线段EF平移至何处时，四边形ABEF的周长最小？求出此时点E的坐标．
粤公网安备 44130202000953号