周日里,我和爸爸、妈妈在家都想使用电脑上网,可是家里只有一台电脑啊,怎么办?为了公平起见我设计了下面的两种游戏规则,确定谁使用电脑上网.
(1)任意投掷两枚质地均匀的硬币,若两枚正面都朝上,则爸爸使用电脑;若两枚反面都朝上,妈妈使用电脑;若一枚正面朝上一枚反面朝上,则我使用电脑.
(2)任意投掷两枚骰子,若点数之和被3整除,则爸爸使用电脑;若点数之和被3除余数为1,则妈妈使用电脑;若点数之和被3除余数为2,则我使用电脑.
请你来评判,这两种游戏规则哪种公平,并说明理由噢!
相关知识点
推荐套卷
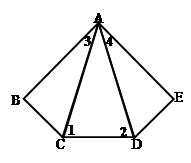
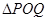 的面积
的面积 .06元的价格按上网时间计费,假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。
.06元的价格按上网时间计费,假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。 选择计费方式能使甲上网费更合算。
选择计费方式能使甲上网费更合算。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号