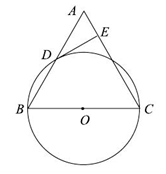
在平面直角坐标系xOy中,已知动点P在正比例函数y=x的图象上,点P的横坐标为m(m>0)。以点P为圆心,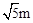 为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
为半径的圆交x轴于A、B两点(点A在点B的左侧),交y轴于C、D两点(D点在点C的上方)。点E为平行四边形DOPE的顶点(如图)。
(1)写出点B、E的坐标(用含m的代数式表示);
(2)连接DB、BE,设△BDE的外接圆交y轴于点Q(点Q异于点D),连接EQ、BQ。试问线段BQ与线段EQ的长是否相等?为什么?
(3)连接BC,求∠DBC-∠DBE的度数。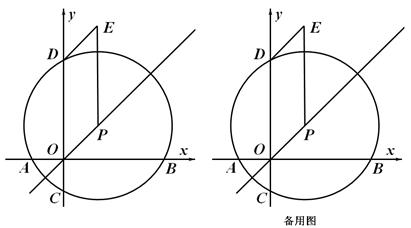
相关知识点
推荐套卷
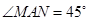 ,
,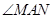 绕点
绕点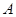 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交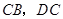 (或它们的延长线)于点
(或它们的延长线)于点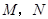 .
.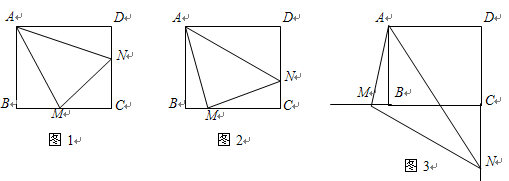
 时(如图1),求证:
时(如图1),求证: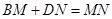 ;
;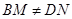 时(如图2),则线段
时(如图2),则线段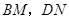 和
和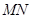 之间数量关系是;
之间数量关系是; 每月能卖出500个.商场想了两个方案来增加利润:
每月能卖出500个.商场想了两个方案来增加利润: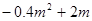 .
.
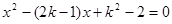 .
.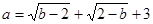
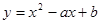 图象与x轴交点坐标;
图象与x轴交点坐标; 粤公网安备 44130202000953号
粤公网安备 44130202000953号